GALVANIC CELL

A Galvanic cell, or Voltaic cell, named after Luigi Galvani, or Alessandro Volta respectively, is an electrochemical cell that derives electrical energy from chemical reactions taking place within the cell. It generally consists of two different metals connected by a salt bridge, or individual half-cells separated by a porous membrane.

Volta was the inventor of the voltaic pile, the first electrical battery. In common usage, the word "battery" has come to include a single Galvanic cell, but a battery properly consists of multiple cells.^[1][2]

History

In 1780, Luigi Galvani discovered that when two different metals (copper and zinc for example) were connected together and then both touched to different parts of a nerve of a frog leg at the same time, they made the leg contract.^[3] He called this "animal electricity". The voltaic pile invented by Alessandro Volta in the 1800s is similar to the galvanic cell. These discoveries paved the way for electrical batteries.

|
Description

Schematic of Zn-Cu galvanic cell

A Galvanic cell consists of two half-cells. In its simplest form, each half-cell consists of a metal and a solution of a salt of the metal. The salt solution contains a cation of the metal and an anion to balance the charge on the cation. In essence the half-cell contains the metal in two oxidation states and the chemical reaction in the half-cell is an oxidation-reduction (redox) reaction, written symbolically in reduction direction as

Mⁿ⁺ (oxidized species) + n e⁻ M (reduced species)

In a galvanic cell one metal is able to reduce the cation of the other and, conversely, the other cation can oxidize the first metal. The two half-cells must be physically separated so that the solutions do not mix together. A salt bridge or porous plate is used to separate the two solutions yet keep the respective charges of the solutions from separating, which would stop the chemical reactions.

The number of electrons transferred in both directions must be the same, so the two half-cells are combined to give the whole-cell electrochemical reaction. For two metals A and B:

Aⁿ⁺ + n e⁻ A

B^m+ + m e⁻ B

m A + n B^m+ n B + m Aⁿ⁺

This is not the whole story as anions must also be transferred from one half-cell to the other. When a metal in one half-cell is oxidized, anions must be transferred into that half-cell to balance the electrical charge of the cation produced. The anions are released from the other half-cell where a cation is reduced to the metallic state. Thus, the salt bridge or porous membrane serves both to keep the solutions apart and to allow the flow of anions in the direction opposite to the flow of electrons in the wire connecting the electrodes.

The voltage of the Galvanic cell is the sum of the voltages of the two half-cells. It is measured by connecting a voltmeter to the two electrodes. The voltmeter has very high resistance, so the current flow is effectively negligible. When a device such as an electric motor is attached to the electrodes, a current flows and redox reactions occur in both half-cells. This will continue until the concentration of the cations that are being reduced goes to zero.

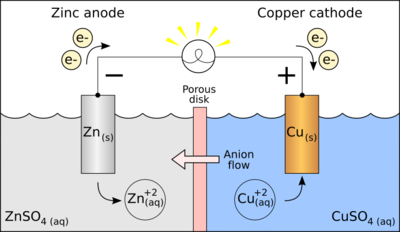
For the Daniell cell, depicted in the figure, the two metals are zinc and copper and the two salts are sulfates of the respective metal. Zinc is the oxidized metal so when a device is connected to the electrodes, the electrochemical reaction is

Zn + Cu²⁺ → Zn²⁺ + Cu

The zinc electrode is dissolved and copper is deposited on the copper electrode (as copper ions become reduced to copper metal). By definition, the cathode is the electrode where reduction (gain of electrons) takes place, so the copper electrode is the cathode. The cathode attracts cations, so has a negative charge when current is discharging. In this case, copper is the cathode and zinc the anode.

Galvanic cells are typically used as a source of electrical power. By their nature they produce direct current. For example, a lead-acid battery contains a number of galvanic cells. The two electrodes are effectively lead and lead oxide.

The Weston cell was adopted as an International Standard for voltage in 1911. The anode is a cadmium mercury amalgam, the cathode is made of pure mercury, the electrolyte is a (saturated) solution of cadmium sulfate and the depolarizer is a paste of mercurous sulfate. When the electrolyte solution is saturated the voltage of the cell is very reproducible, hence its use as a standard.

Cell voltage

The standard electrical potential of a cell can be determined by use of a standard potential table for the two half cells involved. The first step is to identify the two metals reacting in the cell. Then one looks up the standard electrode potential, E⁰, in volts, for each of the two half reactions. The standard potential for the cell is equal to the more positive E⁰ value minus the more negative E⁰ value.

For example, in the figure above the solutions are CuSO₄ and ZnSO₄. Each solution has a corresponding metal strip in it, and a salt bridge or porous disk connecting the two solutions and allowing SO₄²⁻ ions to flow freely between the copper and zinc solutions. In order to calculate the standard potential one looks up copper and zinc's half reactions and finds:

Cu²⁺ + 2 e−
Cu: E⁰ = +0.34 V

Zn²⁺ + 2 e−
Zn: E⁰ = −0.76 V

Thus the overall reaction is:

Cu²⁺ + Zn Cu + Zn²⁺

The standard potential for the reaction is then +0.34 V − (−0.76 V) = 1.10 V. The polarity of the cell is determined as follows. Zinc metal is more strongly reducing than copper metal as shown by the fact that the standard (reduction) potential for zinc is more negative than that of copper. Thus, zinc metal will lose electrons to copper ions and develop a positive electrical charge. The equilibrium constant, K, for the cell is given by

where F is the Faraday constant, R is the gas constant and T is the temperature in kelvins. For the Daniell cell K is approximately equal to 1.5×10³⁷. Thus, at equilibrium, a few electrons are transferred, enough to cause the electrodes to be charged.^[4]

Actual half-cell potentials must be calculated by using the Nernst equation as the solutes are unlikely to be in their standard states,

where Q is the reaction quotient. This simplifies to

where {Mⁿ⁺} is the activity of the metal ion in solution. The metal electrode is in its standard state so by definition has unit activity. In practice concentration is used in place of activity. The potential of the whole cell is obtained by combining the potentials for the two half-cells, so it depends on the concentrations of both dissolved metal ions.

The value of 2.303R/F is 0.19845×10^-3 V/K, so at 25 °C (298.15 K) the half-cell potential will change by 0.05918V / n if the concentration of a metal ion is increased or decreased by a factor of 10.

These calculations are based on the assumption that all chemical reactions are in equilibrium. When a current flows in the circuit, equilibrium conditions are not achieved and the cell potential will usually be reduced by various mechanisms, such as the development of overpotentials.^[5] Also, since chemical reactions occur when the cell is producing power, the electrolyte concentrations change and the cell voltage is reduced. A consequence of the temperature dependency of standard potentials is that the voltage produced by a galvanic cell is also temperature dependent.